
Recently, a new universe model was proposed by Dr. ZHANG Haichao of Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences. His Physical Review D article demonstrates the Universe is a closed space based on the observed concave potential feature of the scalar field shown in the Planck 2018 results.
It is well known that the principle of a homogeneous and isotropic universe is a spatial embodiment of the Copernican principle. The extended Copernican principle indicates further that there is no special space-time position in the Universe. That is, not every part or era of the Universe is the center or the origin. However, suitable initial conditions are required for inflation to start in the current cosmological theory. This starting origin of time is at odds with the extended Copernican principle.
The quasicyclic model resolves the incompatibility with the extended Copernican principle and avoids the fine-tuning of choosing initial conditions for inflation. If the Universe becomes hotter and hotter, the interaction potential well cannot confine quintessence tightly, and then the liberated quintessence results in an extremely rapidly contracting of the Universe due to its large kinetic energy. When the kinetic energy is exhausted, the huge value of the self-interaction potential will drive the Universe inflation. If one is willing to use the term vacuum to describe the field, the vacuum should be called dynamical vacuum rather than static vacuum.
Dr. ZHANG proves that the scalar field can entirely account for the observed late-time cosmic acceleration, due to the symmetry-breaking coupling that can localize the value of the self-interaction potential to act as the cosmological constant.
He shows why his setting can avoid the physical corollary of chameleon no-go theorems and the overshooting problem. Interestingly, his model does not conflict with the no-go theorems, at least mathematically. But the model can break through their unreasonable corollary that the chameleonlike scalar field cannot account for the late-time cosmic acceleration. When the symmetry-breaking coupling with matter is used, the appropriate value of the self-interaction potential can be easily acquired and then drive the late-time acceleration.
As for Weinberg's no-go theorem, since the scheme uses dynamic quintessence rather than static vacuum energy, the no-go theorem is circumvented. In the model, the self-interaction potential of the scalar field has nothing to do with the effective mass around the minimum of the effective potential but can move the position of the minimum. These properties guarantee that the observed cosmic acceleration stems entirely from the coupled scalar field rather than any stable vacuum energy.
When the cosmic constraints are satisfied, the scheme predicts that the magnitude of the fifth force is considerably larger than gravity, especially for lower density in the local environment. However, the fifth force is suppressed into a very short interaction range. Tests of gravity are then satisfied. A typical interaction range is estimated to be about 5 μm for the current matter density of the Universe.
The fifth force might be significantly detectable, provided that experiments are designed that allow test particles to pass through the thin-shell region of sources or at least allow test particles to approach the thin shell as closely as possible.
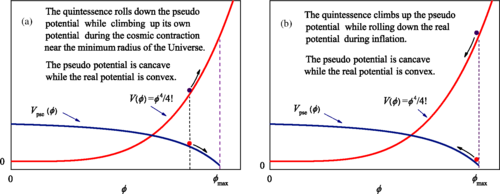
The self-interaction potential and the corresponding pseudopotential near the maximum value of the scalar field. (Image by SIOM)
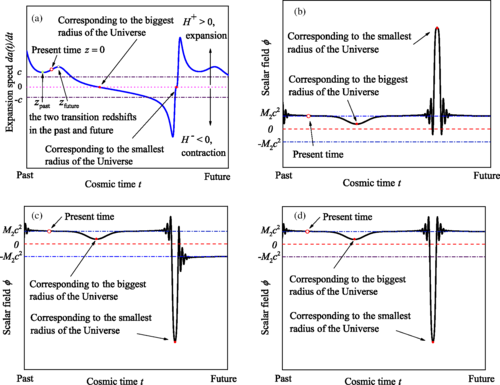
The schematic sketch of the Universe’s evolution with time. (Image by SIOM)

86-10-68597521 (day)
86-10-68597289 (night)

52 Sanlihe Rd., Xicheng District,
Beijing, China (100864)

