Phononic crystals are periodic elastic structures consisting of two different elastic materials, which have the property of band gaps. This property has led to explorations regarding the use of piezoelectric phononic crystals in bulk acoustic wave devices. Compared with bulk acoustic wave devices, surface acoustic wave devices can be used for a greater variety of tasks. Thus, significant research efforts have recently focused on the applications of piezoelectric phononic crystals in surface acoustic wave devices.

Several methods have been developed to analyze surface acoustic wave propagation in piezoelectric phononic crystals, such as finite difference time domain, plane wave expansion, finite element method, and finite element method/boundary element method. However, all these methods show a significant obstacle of large time/memory costs for accurate analysis surface acoustic wave in large size two-dimensional piezoelectric phononic crystals.

To overcome this obstacle, researchers from the Institute of Acoustics (IOA) of the Chinese Academy of Sciences have introduced a novel method of the unit P-matrix and its associated cascading to analyze surface acoustic wave in two-dimensional piezoelectric phononic crystals.

Their research has presented that based on a small unit P-matrix of 25 periods of the phononic crystals, the surface acoustic wave propagation parameters over 150 periods can be accurately obtained using P-matrix cascading. The theoretical and experimental results exhibit good consistency, indicating the accuracy of the unit P-matrix derived by the three-dimensional finite element model, as well as the effectiveness of the P-matrix analysis. The P-matrix analysis of surface acoustic waves in piezoelectric phononic crystals will promote the applications of piezoelectric phononic crystals in surface acoustic wave devices. 

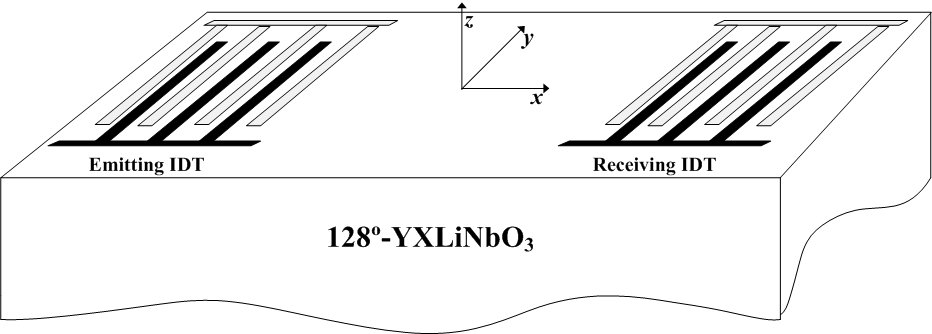
To obtain an accurate unit P-matrix, the Y parameters of the surface acoustic wave delay lines were derived using a three-dimensional finite element model with and without two-dimensional piezoelectric phononic crystals, respectively, on the transmitting path (shown in Fig. 1). A time window function was adopted to extract the desired signals from the P-matrix analysis. In the following, unit P-matrix cascading was used to obtain surface acoustic wave propagation parameters for the large size piezoelectric phononic crystals.  

Using this method, the surface acoustic wave in aluminum (Al) /128º-YXLiNbO3 phononic crystals was analyzed over 150 periods. As well, experiments were conducted to choose the appropriate size of the unit P-matrix and the variance between experimental results and theoretical results. And time/memory cost in different periods were compared as shown in Fig. 2.

Results indicated that cascading by unit P-matrix of 25 phononic crystals periods could be appropriately adopted to accurately derive the surface acoustic wave propagation parameters over 150 periods. Results of unit P-matrix of 25 phononic crystals and the experiments had been shown in the Fig. 3. This showed the accuracy of the unit P-matrix derived by finite element method and the effectiveness of P-matrix analysis. 

In the future, a two-dimensional P-matrix approach will be developed to obtain more accurate results which accounts for considering wave propagation in two directions. 

(a)                                                     (b)

Fig.1 Two surface acoustic wave delay lines: (a) without piezoelectric phononic crystals on the transmitting path; (b) with piezoelectric phononic crystals on the transmitting path (Image by IOA). 

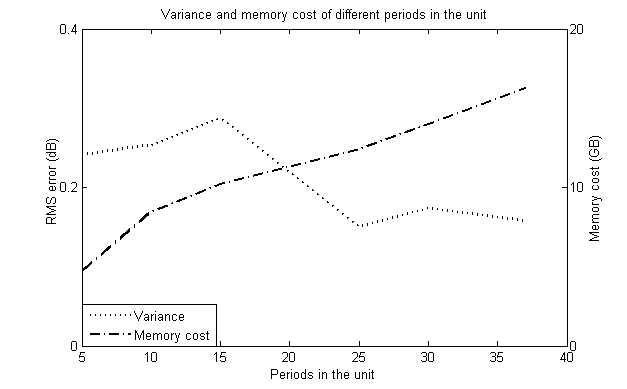
Fig. 2 RMS error and memory cost of different periods in the unit (Image by IOA). 

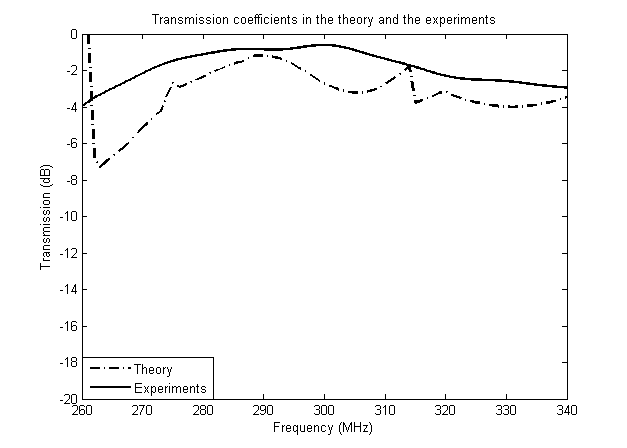
Fig. 3 The theoretical and experimental transmission coefficients (Image by IOA).