
Superconductivity – perhaps the leading example of emergent quantum behavior in matter – was discovered in 1911 but lacked theoretical explanation for almost five decades. In 1957, John Bardeen, Leon Cooper, and John Robert Schrieffer (BCS) developed a microscopic theory of superconductivity1 that came to be known as the BCS theory, which describes superconductivity as a microscopic effect caused by a condensation of Cooper pairs into a boson-like state. BCS theory explains the behavior of what are now known as conventional superconductors – metals for which phonons provide the recently controversial "pairing glue" that leads to the effective attractive quasiparticle interaction responsible for their superconductivity. (Phonons are quantized lattice vibrations, and quasiparticles are mobile electrons or holes in materials; both are quantized elementary excitations.)
As it is wont to do, history is now repeating itself: Unconventional superconductors, in which pairing glue and pairing condensate symmetry differ from conventional superconductors, were discovered in the 1980s – but while it appears from both theory and experiment that electronic spin fluctuations provide the pairing glue for the unconventional superconductivity, a general model remains elusive. Recently, however, scientists at Chinese Academy of Sciences, Beijing and the Santa Fe Institute proposed such a model in the form of an experiment-based phenomenological BCS-like expression for the superconducting transition temperature Tc in heavy-electron materials that is based on a simple model for the effective range and strength of the spin-fluctuation-induced quasiparticle interaction, and reflects the unusual properties of the heavy-electron normal state – in which electrons gain mass as local electron spins lose their magnetism – from which superconductivity emerges.
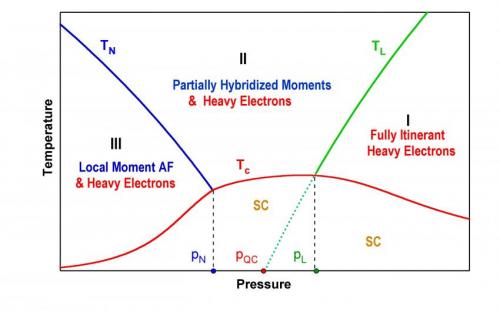
Prof. David Pines discussed the paper that he and Dr. Yi-feng Yang published in Proceedings of the National Academy of Sciences. (Pines and Yang began collaborating in 2007 and have since written nine papers together, with Pines acting as the spokesman for their collaboration.) "The basic challenge we faced was that of exploring new territory – that is, to see whether we could make spin-fluctuation-induced superconductivity more accessible by developing, at a phenomenological level, BCS-like expression for unconventional superconductors that was based on a spin-fluctuation mechanism for their superconductivity," Pines tells Phys.org. (In science, phenomenology describes knowledge based on empirical observations of phenomena that is consistent with, but not derived from, theory.) Pines adds that the scientists decided to start with heavy electron superconductors because these are exceptionally pure; their unusual normal state behavior and how Tc varies with pressure have been studied detail; and, unlike the cuprates, there is a general consensus that antiferromagnetic spin-fluctuations provide the pairing glue for their superconductivity.
The scientists faced several challenges in using a simple model of the effective range and strength of the spin-fluctuation-induced quasiparticle interaction and reflects the unusual properties of the heavy-electron normal state from which superconductivity emerges to develop a BCS-like equation for Tc in heavy-electron materials, the first being providing a quantitative explanation of the measured pressure-induced variation in Tc in the heavy-fermion superconducting so-called "hydrogen atoms" of unconventional superconductivity – cerium-cobalt-indium 5 (CeCoIn5) and cerium-rhodium-indium 5 (CeRhIn5). "Explaining that variation is a significant measure of the success of any proposed model of their superconductivity, so we were delighted to find that we could provide the explanation of that variation by further specifying that for a given material, the range of energies over which a quantum critical spin-fluctuation induced interaction will be attractive must be proportional to its coherence temperature, T*, at the pressure pL, at which Tc is maximum."

Secondly, their model predicts a similar pressure variation for other heavy-electron quantum critical superconductors. "A good model or theory not only explains past measurements, but has predictive capabilities," Pines points out. "Therefore, a key further test of our BCS-like expression is its prediction that a measurement of the variation of Tc with pressure in additional heavy electron materials will show a dome-like structure, with the maximum in Tc occurring at the pressure at which localization sets in."
A crucial further test, Pines continues, was that the model quantifies their variations in Tc with a single parameter. "Once one fixes, at a given pressure, the material-sensitive parameter that measures the relative effectiveness of the attractive spin-fluctuation induced interaction in bringing about superconductivity, then there are no free parameters left in our BCS-like expression for the superconducting transition temperature at other pressures."
To address these challenges, Pines notes that the two-fluid model that yields correct specific heat results for a number of heavy-electron compounds was central to understanding both the unusual normal state properties of heavy electrons3, as well as their superconductivity. "The two-fluid model provides a simple and successful phenomenological model for the emergence of heavy electron behavior at T*, including the magnitude and logarithmic temperature variation of the specific heat produced by heavy electron density," Pines explains. "It also led to the discovery of universal scaling behavior with T*, while careful measurements of the single ion Kondo effect showed that the physical origin of T* is the interaction between the nearest neighbor local moments whose collective hybridization with the background conduction electrons leads to the emergence of heavy electron behavior in the normal state." (The Kondo effect describes the scattering of conduction electrons by single magnetic impurities in a metal, resulting in a characteristic change in electrical resistivity with temperature.)
The scientists determined that in the case of CeCoIn5, the range of the effective attractive interaction found in microscopic strong coupling calculations is remarkably close to what they proposed phenomenologically. "Making this comparison is a very important check on our phenomenology," Pines says. "In carrying it out, we extrapolated the results from a study of microscopic strong coupling calculations of spin-fluctuation-induced superconductivity in the cuprates4, where it was found that a BCS-like expression could parameterize their numerical results quite well, to heavy electrons."
Pines says that the question of whether their phenomenological approach can be extended to the cuprates and any other unconventional superconductors in which scaling behavior for the spin-lattice relaxation rate with Tc has been seen at or near optimal doping levels "is a very interesting and important question, and one we are currently trying to answer. For the cuprates, one can be guided by the strong coupling microscopic calculations and nuclear magnetic resonance (NMR) experiments that enable one to determine the range of the attractive interaction at optimal doping." (In NMR, nuclei in a magnetic field absorb and re-emit electromagnetic radiation.) "What's less clear is the doping dependence of the density of states and the coupling strength g, which together will fix the dome structure seen experimentally. We find we can choose these in such a way as to yield this structure, but would like to be able to relate that straightforward phenomenology to experiments on the magnetic properties in the normal state. That is a work in progress."
Currently, Pines tells Phys.org, the scientists are working on two projects: extending to the cuprates their phenomenological approach to quantum critical spin-fluctuation-induced superconductivity in heavy-electron materials, and – in further collaboration with Gilbert Lonzarich5,6,7 at Cambridge University – writing a perspective on basic concepts in heavy electron physics exploring why it has proven so difficult to develop a microscopic theory of the emergence and subsequent behavior of heavy electrons in Kondo lattice materials."
"Our successful phenomenological approach to emergent behavior in heavy electron materials can serve as a guide to developing a microscopic theory of that behavior," Pines concludes. "It also provides an example of how to deal with the challenging problems posed by the emergent behavior found in other strongly correlated electron materials: First, use experiment as a guide to develop a consistent phenomenological model that incorporates the organizing principles that might be responsible for that behavior; second, then and only then, try to devise and solve a simple microscopic model that incorporates these organizing principles and provides results that can be compared with experiment." (Phys.org)

86-10-68597521 (day)
86-10-68597289 (night)

52 Sanlihe Rd., Xicheng District,
Beijing, China (100864)

